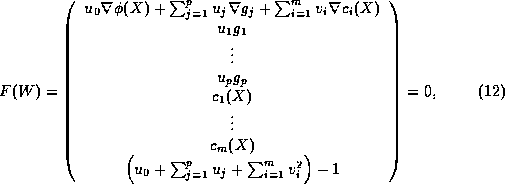
where
Critical points of the constrained optimization
Problem 2 are zeros of the
Fritz-John system defined by
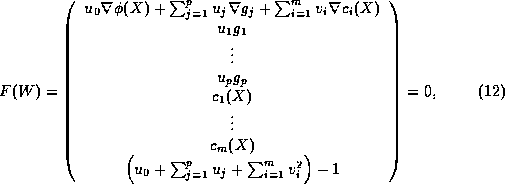
where ![]() ,
, ![]() , the
, the ![]() are unconstrained, and
the last equation is one of several possible normalization conditions.
For details, see [6, §10.5,] or
[8, §5.2.5,].
are unconstrained, and
the last equation is one of several possible normalization conditions.
For details, see [6, §10.5,] or
[8, §5.2.5,].
An interval Newton method applied to the system (12)
is used within GlobSol to narrow the size of the boxes ![]() considered
within the overall algorithm. The bound constraints are included
by applying the interval Newton method within a
reduced space, that is, by treating boxes with active bound
constraints separately, and fixing variables corresponding to active
bound constraints. Similarly, inequality constraints that are
certainly feasible (i.e. those
considered
within the overall algorithm. The bound constraints are included
by applying the interval Newton method within a
reduced space, that is, by treating boxes with active bound
constraints separately, and fixing variables corresponding to active
bound constraints. Similarly, inequality constraints that are
certainly feasible (i.e. those ![]() for which the interval extension
for which the interval extension
![]() , and, hence, for which
, and, hence, for which ![]() ) are removed from the
Fritz-John system. The current interval bounds for U and V
are associated with each box
) are removed from the
Fritz-John system. The current interval bounds for U and V
are associated with each box ![]() , and are inherited by sub-boxes
if
, and are inherited by sub-boxes
if ![]() is subdivided.
is subdivided.
The verification properties of the interval Newton method can, in theory, be used to verify existence of a feasible critical point. However, the overall branch and bound algorithm often only needs verification of a feasible point within a particular small box. Approximate feasible critical points are sometimes much harder to obtain than approximate feasible points. Similarly, an alternate verification procedure (see §8) is more robust than using the Fritz-John system to merely verify the existence of feasible points.