When the expressions defining the objective function, gradient, and constraints are evaluated, intermediate quantities are computed. Under certain circumstances, the relationships among these intermediate quantities can be used, other than in the straightforward way for evaluating the dependent variables, to obtain tighter bounds on the dependent variables or to obtain a conclusion that no optimum can exist within the given box.
For example, suppose
is to be optimized over
.
The global optimum of 
over 
is 0, and the unique
optimizer is 
. If is programmed as
T(1) = X(1)**2
T(2) = X(2)**2
PHI(1) = T(1) - T(1)*T(2) + T(2)
then an early version of GlobSol, compiled with the NAG compiler version 2.1, produces the following list of intermediate operations.
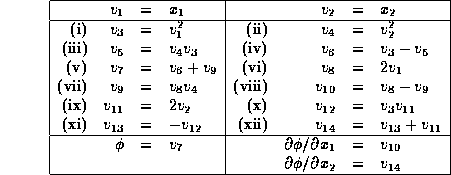
(Different compilers will produce different decompositions,
or code lists.)
Suppose we know a sharp upper bound 
on the global
optimum, and suppose the sub-box
is to be processed. An initial evaluation
of the code list (i.e. a forward substitution) gives:
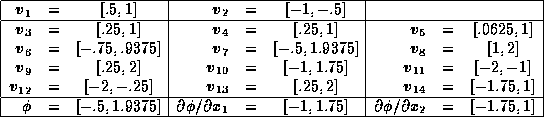
Thus, since 
and 
, the
box cannot be rejected just from the computed values. However,
we may set 
, and solve for 
in (v):
We may now solve for 
in (viii), obtaining
Since 
(with 
),
cannot contain both the global optimum and a critical point
of . Thus, the box 
may
be rejected.