In GlobSol, bound constraints are handled with the "peeling" process
described in [8, §5.2.3,]. In this process, edges of
the initial box 
are marked as bound constraints in the box
data file. For instance, the box data file may contain the information
1.D-10 ! Domain tolerance -2 2 ! Search region limits on the first variable X(1) -3 3 ! Search region limits on the second variable X(2) -4 4 ! Search region limits on the third variable X(3) T F ! X(1)>= -2 is a bound constraint F F ! No bound constraints on X(2) T T ! X(3)>=-4 and X(3)<=4 are both bound constraints
In the peeling scheme, GlobSol produces six initial boxes, consisting
of the original box
and the five
degenerate boxes
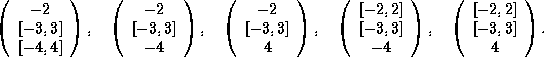
The interval Newton method proceeds in lower-dimensional spaces
(dimension 2 or dimension 1 in the cases above) on the degenerate
sub-boxes. Degenerate boxes are otherwise handled similarly to any
other boxes in the branch and bound procedure. Various details in
the algorithm prevent redundancy, etc.
This peeling scheme can be the most efficient way of posing the problem when there are a small number of bound constraints, but the amount of computation can increase geometrically as the number of bound constraints increases. It may be better to pose bound constraints as inequality constraints if there are a large number of bound constraints; the user should experiment.